ЗОЛОТОЕ  СЕЧЕНИЕ

На протяжении многих веков, для построения гармоничных композиций художники пользуются понятием "Золотое сечение".

В наше время трудно поверить, что лириче­ское начало художественного творчества может свободно уживаться с точной наукой. Однако выдающиеся мастера былых эпох, в первую оче­редь античности и Возрождения, постоянно стре­мились проверить алгеброй гармонию, обуздать (а значит - и обогатить) творческие эмоции точ­ным, почти математически достоверным расче­том. Ни один шаг в их работе не обходился без опоры на учение о пропорциях, которое, напри­мер, при построении человеческих фигур форму­лировалось в виде точных таблиц идеальных соотношений.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деленияпозаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуютзолотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Впрочем, математика античности, средневековья и Возрождения была лишена сухости и абстракт­ности: подробное учение о символике чисел наделяло их философским, религиозным и даже эстетическим смыслом. Почетное место в ряду символических величин занимало золотое сечение, олицетворяющее равновесие знания, чувств и силы. Это иррациональное соотношение (0,618) возни­кает при делении отрезка на две неравные части, при котором весь отрезок относится к большей его части, как большая к меньшей. Открытие пропорций, видимо, принадлежит к за­слугам древневосточной математики, античная же традиция связывает его с именем выдающегося математика VI века до н. э. Пифагора и его уче­ника Никомаха. 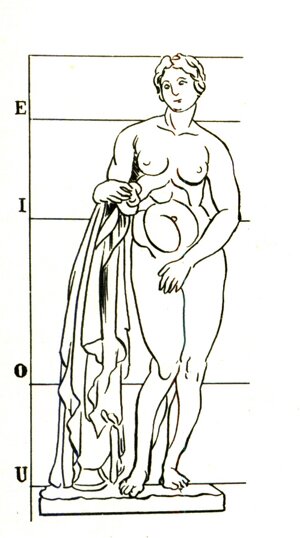Знакомство с золотым сечением сыграло немалую роль в работе античных архи­текторов и скульпторов. Будет интересно узнать правило, наглядно прослеживающееся в древне­греческих статуях: при делении туловища чело­века в соответствии с золотым сечением легко найти уровень пупа и локтя, при повторном деле­нии двух отрезков в противоположных направле­ниях обнаруживается высота колена и нижний уровень шеи.

В средние века изучение золотого сечения обо­гатилось работами Леонардо Пизанского, про­званного Фибоначчи,— выдающегося итальянско­го математика XIII века. Создав бесконечный ряд, в котором каждое следующее число являет­ся повторением двух предыдущих (1, 2, 3, 5, 8, 13, 21...), он установил, что соотношение соседних чисел близко к пропорции золотого сечения. За­мечательными свойствами обладает прямоуголь­ник, стороны которого соответствуют числам Фибо­наччи. При его делении на квадрат и другой пря­моугольник последний сохраняет то же соотно­шение сторон. Выдающийся немецкий астроном XVI—XVII веков И. Кеплер сравнивал феноме­нальное воспроизведение пропорции самое себя со способностью Бога «творить подобное из подоб­ного».

Хорошо известная в эпоху Возрождения, эта пропорция вплоть до середины прошлого столетия была почти забыта, и уже в нынешнем веке вновь изучена рядом ученых и архитекторов. Особую роль среди них сыграл французский зодчий Ле Корбюзье, создавший гак называемый модулор - систему деления человеческой фигуры на согла­сованные в золотом сечении отрезки от ступни до талии, от талии до затылка и от затылка до верх­них пальцев поднятой руки.

...Старые мастера любили окутывать свои рабо­ты завесой тайны, и нередко замечательная про­порция оказывается путеводной нитью, позволяю­щей вторгнуться в богатый мир творческих замы­слов художника. Однако распознать золотое сечение бывает порой очень непросто. Так, на кар­тине крупного итальянского живописца и мате­матика XV века Пьеро делла Франчески «Биче­вание Христа» в мраморной плите пола, укра­шающей портик, обнаруживается сложный гео­метрический узор, который включен в систему линейной перспективы и потому воспринимается искаженным. Представив этот чертеж как вид сверху, получим прямоугольник, построенный с использованием золотого сечения: сочетание раз­личных элементов чертежа заставляет вспомнить математические задачи Фибоначчи, прекрасно известные художнику. В итоге перед глазами зрителя предстает замечательная восьмиугольная звезда, которая обладает как художественной красотой, так и математическим совершенством. Обычный зритель никогда ее не увидит, а уче­ный-математик, который подойдет к картине с линейкой и внимательно изучит чертеж, неожи­данно обнаружит «скрытую» красоту.

Пример многократного использования золотого сечения предлагает другой замечательный худож­ник той же эпохи - Антонелло да Мессина - в знаменитой картине «Святой Себастьян». Эта про­порция, во-первых, лежит в основе трактовки тела святого. Но подлинные чудеса раскрывают­ся при взгляде на изображения заднего плана. Воин в высокой шапке, видимо, такого же роста, как и Себастьян, держит копье, древко которо­го достигает его макушки. Очевидно, что соглас­но тому же стандарту изготовлено и другое копье, оказывающееся явно не по росту лежащему рядом и человеку: его древко перекинуто между двумя уровнями высоты. Подробные вычисления, опи­рающиеся на пропорции человеческой фигуры и теорему Пифагора, а также учитывающие длину обоих копий, обнаруживают, что плитки пола являются прямоугольниками, стороны которых находятся в золотом соотношении. И это неожи­данно наталкивает на целую гамму прекрасно задуманных пропорций. Рост лежащего воина, который мы можем установить по длине его вытя­нутой вперед левой стопы, в соотношении с ро­стом Себастьяна даст квадратный корень золотого сечения — 0,79. И если святой является атлетом в 6 футов (1 м 80 см — 1 м 90 см), то лежащий воин оказывается карликом, достигающим 1 м 40 см -  1 м 50 см. Квадрат золотого сечения (0,38) создается отношением диаметра к высоте обломка колонны символа ранней смерти, лежащего на переднем плане. А если мы поста­вим обломок рядом с ногой Себастьяна, то он окажется на уровне его колена, что также связа­но с замечательной пропорцией. Богатая фанта­зия художника, соединенная с аналитической ясностью замысла, свидетельствует, что золотое сечение полностью оправдывает свое назначение, установленное еще в эпоху Пифагора,— создавать равновесие знания, чувств и силы.

Как и Антонелло да Мессина, Рафаэль не был ученым-математиком, но, подобно многим худож­никам той эпохи, обладал немалыми познания­ми в геометрии. В знаменитой фреске «Афинская школа», где в храме науки предстоит общество великих философов древности, наше внимание привлечет группа Эвклида - крупнейшего древ­негреческого математика, разбирающего сложный, чертеж. Хитроумная комбинация двух треугольников также построена в соответствии с пропор­цией золотого сечения: она может быть вписана
в прямоугольник с соотношением сторон 5/8. Этот чертеж удивительно легко вставляется в
верхний участок живописной архитектуры. Верх­ний угол треугольника упирается в замковый камень арки на ближнем к зрителю участке, нижний — в точку схода перспектив, а боковой участок обозначает пропорции пространственного разрыва между двумя частями арок. И не слу­чайно в облике живописного Эвклида обнару­живается портрет друга Рафаэля, известного архитектора Браманте, участвующего в разработке проекта согласно тем математическим и художественным законам, которые установ­лены персонажами фрески учеными антич­ного мира.

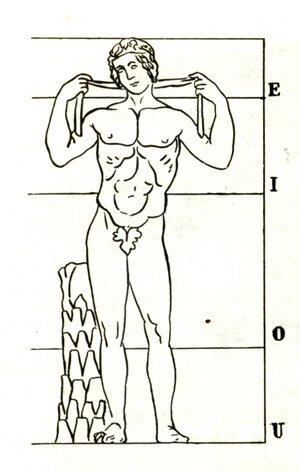Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией».

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

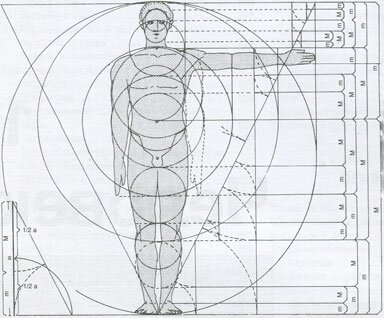В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет:

«Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

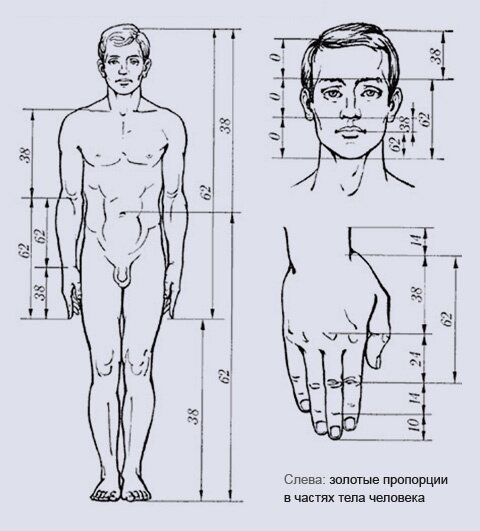Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Золотое сечение можно найти и в анатомии. Закон золотого сечения просматривается в количественном членении человеческого тела, соответствующем числам ряда Фибоначчи. Примером может быть число костей туловища, черепа и конечностей. Так, в скелете туловища различают 3 костных системы: позвоночник, реберный его отдел и грудину. Грудина включает 3 кости (рукоятку, тело и мечевидный отросток). Позвоночник состоит из 33 (34) позвонков; от них отходят 12-13 пар ребер.

Мозговой череп состоит из 8 костей. В верхней и нижней челюстях с каждой стороны имеется по 8 альвеол и соответственно - корни 8 зубов.

Скелет верхней конечности состоит из 3 частей (плечевой, костей предплечья и костей кисти). Кисть включает 8 костей запястья, 5 пястных костей и кости 5 пальцев. Каждый палец, кроме большого, имеет по 3 фаланги. Таким образом, морфогенез кисти, включающей два соседних члена числового ряда Фибоначчи - в частности, 8 костей запястья и 5 костей пясти - приближается к золотому сечению 1.618, поскольку 8/5=1.6.

Сопоставляя длины фаланг пальцев и кисти руки в целом, а также расстояния между отдельными частями лица, также можно найти "золотые" соотношения.

Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении золотого сечения. Измерения нескольких тысяч человеческих тел позволили обнаружить, что для взрослых мужчин это отношение равно в среднем примерно 13/8 = 1,625, а для взрослых женщин оно составляет 8/5 = 1,6. Так что пропорции мужчин ближе к "золотому сечению", чем пропорции женщин (однако женщина в обуви на каблуках может оказаться ближе к "золотым" пропорциям). У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году у мужчин равняется 1,625. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Деятельность сердца связана с периодической сменой двух противоположных, функционально дополняющих друг друга состояний сердечной мышцы - систолы (напряжения) и диастолы (расслабления). Установлено, что для каждого вида животных существует частота сердцебиений.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.

В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

А. Эйнштейн, прочи­тавший книгу Корбюзье «Модулор», написал письмо архитектору, в котором есть замечательные слова:

«Это гамма пропорций, которая делает плохое трудным и хорошее легко достижимым».

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.